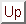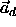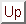
The motion of the Huygens Probe in Titan's atmosphere
is determined by the action of two forces, gravity and wind drag.
The acceleration due to wind
drag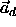 
is taken from Flury (1986) to be:
where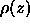 
is the atmospheric density,
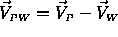is the relative velocity of the
Probe with respect to the atmospheric wind,
and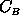 
is the ballistic coefficient
(units: kg/mē) defined by:
with m = probe mass, 
drag coefficient,
and A = effective probe area to the flow.
The wind velocities in the (x,y,z) directions of a Cartesian
coordinate system on Titan's surface are given by:
u = zonal wind (x-axis: positive toward east)The Probe's equation of motion during the Titan descent phase can thus be written:v = meridional wind (y-axis: positive toward north)
w = vertical wind (z-axis: positive upwards)
where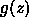 
is Titan's gravitational acceleration, and
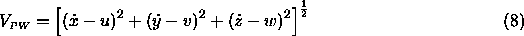
The meridional and vertical winds, v and w, are assumed to be considerably weaker than the zonal wind u. In this case, the latitude of the Probe (y component) remains approximately constant.
Knowing the Probe's velocity on Titan, it is not difficult to determine the Doppler shift projected onto the PRL ray path back to the Orbiter:
where
with
The vector
= probe velocity w.r.t. Titan center
= orbiter velocity w.r.t Titan center
= unit vector pointing from Orbiter to Probe
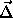defines the line-of-sight of the PRL.
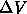is negative during the Titan descent, so that
the received frequency is increased (blue shifted).
The PRL Doppler shift (9) is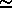 
37.6 kHz for
the nominal orbiter starting approach velocity of -5.53 km/s.
The velocity of the Probe projected onto the line-of-sight
can be written:
where
Furthermore, we define the projection of the orbiter velocity onto the line-of-sight by:
The angles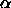 
and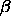 
define the direction from the Probe
to the Orbiter in a local Cartesian coordinate system on the Probe
oriented along a natural Titan coordinate grid
(x-axis positive toward east;
y-axis positive toward north; z-axis positive upward).
The angle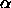 
, basically the zenith angle of the Orbiter
as seen from the Probe (Ott 1991), is also sometimes designated as the
"probe aspect angle" (PAA).
The azimuthal angle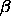 
of the Probe-to-Orbiter line-of-sight
is labeled the "line-of-sight azimuth" (LOSA) by
some authors (Atkinson 1989, Pollack et al. 1992).
The term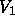 
in (12), where the mean value of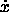 
u, the drift velocity due to zonal winds,
is the quantity to be determined by DWE.
This velocity is co-aligned with the contribution
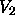in (13) due to Titan rotation.
It is assumed for simulation purposes that the rotation is
synchronous with the Titan orbital period
(
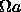
11.7 m/s).
As noted in the previous section, the relative importance of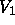 
,
and thus the quality of the reconstructed wind profile,
is strongly dependent on the values of 
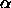and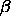 
.
The term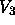 
in (14), arising from meridional drift,
should be small since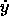 
is not expected to be important.
The term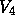 
in (15) contains
the vertical descent velocity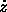 
.
This quantity can be obtained to a high degree of accuracy either
from the range rates deduced from the Probe's proximity sensor data,
or using measurements of temperature T and pressure P from the
Huygens Atmospheric Structure Instrument (HASI).
In the latter case, based on the assumption of hydrostatic
equilibrium and ideal gas behavior, the descent velocity is
determined from
where variations in H =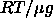 
, the atmospheric scale height,
are assumed to be negligible over the altitude range
of the Huygens descent.
The final error associated with the determination of
the reconstructed probe descent velocity is estimated to be
of the order of 1%.
Knowing 
from the proximity sensor or from HASI
measurements, it is possible to reconstruct 
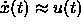from the Doppler shift of the PRL (9).
Using in situ measurements of the density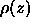 
,
we can then extract the exact height profile 
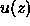from the
motion equations (5) and (7).
Comparitive wind measurements are expected near the surface from two
independent sources on board the Huygens Probe:
In order to provide a rough estimate of the Doppler shifts involved,
Fig. 4 shows the results of a simplified calculation
of the five line-of-sight velocity contributions
to the PRL frequency shift,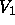 
through 
.
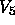The geometry for the calculations was taken from the nominal
Huygens descent profile on Titan (duration: 135 min).
The upper and lower panels show the same curves on different
ordinate scales.
Figure 4: Velocity contributions to PRL
Doppler shift for the nominal Huygens descent profile.
Only the change in the projected orbiter velocity from its
initial value, i.e.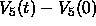 
, is plotted in
Fig. 4.
The total projected velocity is plotted for the other contributions,
all of which happen to be negative
(blue shift in PRL frequency) in this example.
The 100% nominal zonal wind model was used for computing the
zonal wind contribution 
.
The Titan rotation term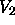 
is nearly constant during
the entire descent.
The meridional winds in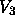 
were taken to be a constant
+1 cm/s (blowing toward north).
The change of parachutes at t = 15 min is clearly seen in the
curve for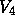 
, which is the second largest contributer to the
changing Doppler shift.
In addition to the derivation of a zonal wind height profile from
the large-scale drift, DWE may be able to provide valuable science
and navigation services from the small-scale variations in frequency
as a 'by-product' of the analysis.
Two such possibilities are:
)
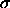of 
= 
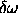0.27/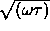
rpm,
where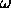 
is
the spin rate in rpm and 
is the integration time in minutes.
For a representative value of 
= 1 min,
this yields a relative error of 27% just prior to impact,
when the probe spin rate is expected to be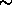 
1 rpm.
The relative error is much smaller at higher altitudes where the
spin rate is greater (e.g., 
0.9% for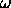 
= 10 rpm,
= 1 min).
An improvement in this estimate from the Doppler data can be achieved
by including the signal level data.
Because the radiation pattern of the Probe Transmitter Antenna (PTA)
is asymmetric, the Probe's rotation phase can be determined from the
phase of the received signal level modulation.
The amplitude of PTA's cyclic variation will be ca. 
2 dB
during each rotation.
