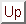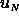 at a specific time
at a specific time
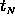 , must be determined by independent means.
This problem does not exist with the Huygens DWE because the
absolute fractional frequency uncertainties inherent to the TUSO and
RUSO are of the order
, must be determined by independent means.
This problem does not exist with the Huygens DWE because the
absolute fractional frequency uncertainties inherent to the TUSO and
RUSO are of the order 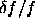
 2·10E-10.
2·10E-10.

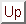

A robust zonal wind recovery algorithm for the Cassini-Huygens scenario has been developed by Atkinson et al. (1990). Much of the formalism has been carried over from the experience gained from a very similar DWE investigation on the Galileo Mission (Pollack et al. 1992). An essential prerequisite to application of the algorithm is an accurate reconstruction of the probe-orbiter relative geometry. It is initially assumed that the Probe's position is not affected by the integrated effect of the winds. Once a preliminary wind profile is calculated, the probe descent position can be updated to reflect the integrated effect of the winds on the probe descent longitude, and the wind profile is recalculated with the new time-varying probe longitudes. An important assumption is that the zonal winds are dominant, with the possible exception of the last few kilometers above the surface.
The zonal wind profile derived from the DWE measurements on Galileo
is a relative (wind shear), rather than absolute profile.
This is because of the rather large uncertainty in the actually
transmitted frequency from the quartz USO on the Galileo Probe.
The "constant" of the integration, i.e. a value of the wind
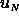 at a specific time
at a specific time
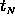 , must be determined by independent means.
This problem does not exist with the Huygens DWE because the
absolute fractional frequency uncertainties inherent to the TUSO and
RUSO are of the order
, must be determined by independent means.
This problem does not exist with the Huygens DWE because the
absolute fractional frequency uncertainties inherent to the TUSO and
RUSO are of the order 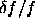
 2·10E-10.
2·10E-10.
Under these circumstances, the accuracy with which the zonal winds can be recovered is determined by the imperfect knowledge of the Probe/Orbiter trajectory. Of lesser importance are second-order Taylor, Doppler and Special Relativistic terms that are usually dropped in order to keep the recovery problem linear, and environmental effects due to S-band signal propagation through a refracting, attenuating atmosphere (e.g. Bird 1995). Trajectory and oscillator drift errors introduce a small time-varying component into the probe-orbiter relative velocity that cannot be distinguished from atmospheric winds. A detailed treatment of the effects of these various errors for the recovery of the zonal wind height profile may be found in Atkinson et al. (1990).
In order to better understand the limitations of the recovery algorithm, we numerically simulated the wind recoveries for a variety of different trajectories, wind environments and errors. Here we summarize the results from several of those simulations and compare the recovered wind profile to the ideal case, where no frequency errors, trajectory uncertainties or anomalous wind regions exist. In all cases the input wind profile is a "Flasar-type" model, a linearly increasing zonal wind with height, the direction and magnitude of which are variable parameters of the simulation. Wind recovery results for four different models are shown in Fig. 5 after five iterations.
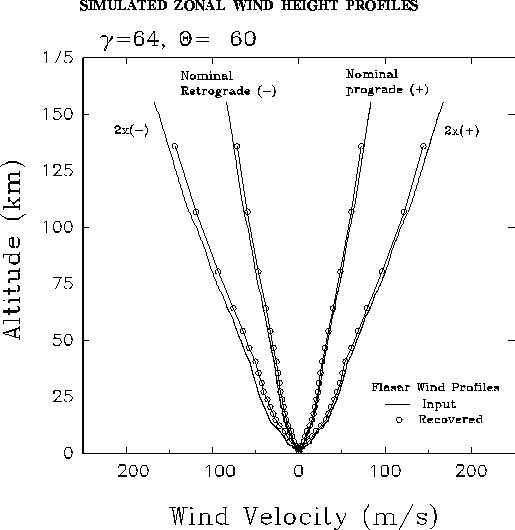
Figure 5: Height profiles of input and
recovered zonal wind velocities.
The input errors used in the simulations of Fig. 5 were
representative for the Huygens descent on Titan.
The largest error sources are those due to
probe entry longitude (0°.7), probe entry latitude
(0°.1), probe descent velocity (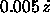 ),
and the maximum possible USO frequency drift (0.4 Hz in 2.5 hours).
In spite of the nonnegligible trajectory and frequency errors,
the recovered wind profiles in Fig. 5 are very good
facsimilies of the input profiles.
Differences are only apparent in the upper levels of the
atmosphere on the scale of the graph.
The errors decrease during the probe descent - in these simulations
constrained to be zero at Titan's surface.
),
and the maximum possible USO frequency drift (0.4 Hz in 2.5 hours).
In spite of the nonnegligible trajectory and frequency errors,
the recovered wind profiles in Fig. 5 are very good
facsimilies of the input profiles.
Differences are only apparent in the upper levels of the
atmosphere on the scale of the graph.
The errors decrease during the probe descent - in these simulations
constrained to be zero at Titan's surface.
The touchdown longitude 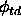 is located about 6°
(260 km) east of the entry longitude for the case with the nominal
prograde wind profile.
The mean speed of the Probe in its easterly drift is
is located about 6°
(260 km) east of the entry longitude for the case with the nominal
prograde wind profile.
The mean speed of the Probe in its easterly drift is
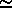 100 km/hr (28 m/s).
Since the drift speed can be higher than the vertical descent velocity,
the flight path to the surface can become rather flat.
As expected from (7), the vertical descent time is only weakly
dependent on the zonal wind u.
100 km/hr (28 m/s).
Since the drift speed can be higher than the vertical descent velocity,
the flight path to the surface can become rather flat.
As expected from (7), the vertical descent time is only weakly
dependent on the zonal wind u.
The quality of the wind recovery for the 4 examples of
Fig. 5 is summarized in Table 2, which
shows (a) the mean error in the determination
of the zonal wind over the height interval 0-100 km (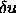 in
m/s), and (b) the error in the determination of the
impact longitude (
in
m/s), and (b) the error in the determination of the
impact longitude (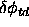 in degrees).
in degrees).
Additional simulations verified that the wind recovery algorithm is not affected by an input wind profile with a region of high shear, i.e., the wind recovery is not limited to smooth and slowly varying horizontal winds. As noted in the previous section, however, the detectability of fine wind structure is limited by the probe response time (20).